回归分析

理论

• 预测变量X，Predictor
• 响应变量Y，Response
• 截距，常数 $$ \beta_0 $$，Intercept
• 斜率，Slope
• 统计误差
• 估計係數，Estimate Coefficient.
• 惩罚因子

普通线性模型(ordinary linear model)

Y=β0+β1x1+β2x2+…+βp−1xp−1+ϵ 这里βi，i=1,…,p−1称为未知参数，β0称为截矩项。

普通线性模型的假设主要有以下几点：

1. 响应变量Y和误差项ϵ正态性：响应变量Y和误差项ϵ服从正态分布，且ϵ是一个白噪声过程，因而具有零均值，同方差的特性。
2. 预测量xi和未知参数βi的非随机性：预测量xi具有非随机性、可测且不存在测量误差；未知参数βi认为是未知但不具随机性的常数，值得注意的是运用最小二乘法或极大似然法解出的未知参数的估计值β^i则具有正态性。
3. 研究对象：如前所述普通线性模型的输出项是随机变量Y。在随机变量众多的特点或属性里，比如分布、各种矩、分位数等等，普通线性模型主要研究响应变量的均值E[Y]。
4. 联接方式：在上面三点假设下，对(1.1)式两边取数学期望，可得 E[Y]=β0+β1x1+β2x2+…+βp−1xp−1 可见，在普通线性模型里，响应变量的均值E[Y]与预测量的线性组合β0+β1x1+β2x2+…+βp−1xp−1通过恒等式(identity)联接，当然也可认为通过形为f(x)=x的函数(link function)联接二者，即 E[Y]=f(β0+β1x1+β2x2+…+βp−1xp−1)=β0+β1x1+β2x2+…+βp−1xp−1

OLS

残差平方和最小

类型：

• 简单线性回归
• 多元线性回归
• 多项式

經驗：

• log-linear：如果散點圖呈現對數格式，則取對數log(Predictor)，可以提高R^2.
• qqnorm，查看Residual是否为正态线
• plot(lm$residual,lm$fitted.values)，查看是否为无模式。

简单线性回归

用一个量化的解释变量预测一个量化的响应变量。

> fit <- lm(weight ~ height,data=women)
> summary(fit)

Call:
lm(formula = weight ~ height, data = women)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.7333 -1.1333 -0.3833  0.7417  3.1167 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -87.51667    5.93694  -14.74 1.71e-09 ***
height        3.45000    0.09114   37.85 1.09e-14 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared:  0.991,    Adjusted R-squared:  0.9903 
F-statistic:  1433 on 1 and 13 DF,  p-value: 1.091e-14

Residuals：残差，呈Q-Q分布最好 Coefficients：相关性 Intercept：截距 P值：越小越重要，影响越显著，1-p表示影响的程度。

> women$weight
 [1] 115 117 120 123 126 129 132 135 139 142 146 150 154 159 164
> fitted(fit)
       1        2        3        4        5        6        7        8        9 
112.5833 116.0333 119.4833 122.9333 126.3833 129.8333 133.2833 136.7333 140.1833 
      10       11       12       13       14       15 
143.6333 147.0833 150.5333 153.9833 157.4333 160.8833 
> residuals(fit)
          1           2           3           4           5           6           7 
 2.41666667  0.96666667  0.51666667  0.06666667 -0.38333333 -0.83333333 -1.28333333 
          8           9          10          11          12          13          14 
-1.73333333 -1.18333333 -1.63333333 -1.08333333 -0.53333333  0.01666667  1.56666667 
         15 
 3.11666667 
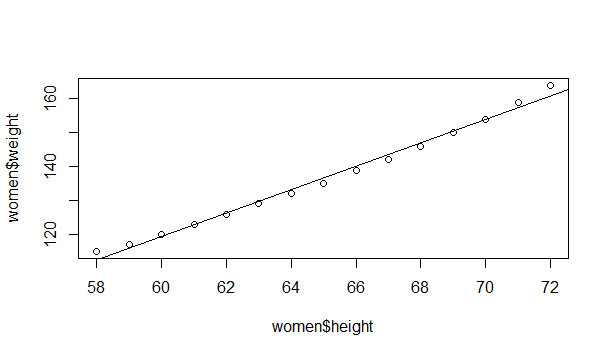
> plot(women$height,women$weight)
> abline(fit)

多元线性回归

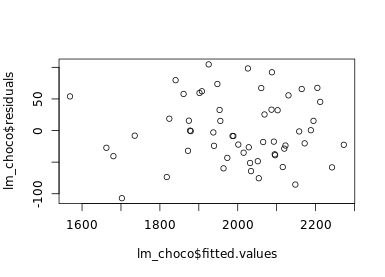
拟合值与残差的分布：

# Plot the residuals in function of your fitted observations
plot(lm_choco$fitted.values,lm_choco$residuals,data=lm_choco)

残差的Q-Q图：

> qqnorm(lm_choco$residuals)