SVM

1. 理论

线性分类器

所谓线性分类器即用一个超平面将正负样本分离开，表达式为 y=w*x ，这里是强调的是平面；而非线性的分类界面可以是曲面，多个超平面的组合等。

超平面hyper plane

N维空间的平面： w *x + b = 0

logistic回归

logistic函数（或称作sigmoid函数）。在生物学中常见的S型的函数，也称为S型生长曲线。

  S(x) = (1+ e^-x)^-1

其取值的极限为(0,1)。

函数间隔

几何间隔

距离公式。 大间隔分类器Maximum Margin Classifier

核函数kernel

2. 示例

data(iris) # 1
attach(iris) # 2

## classification mode
# default with factor response:
model <- svm(Species ~ ., data = iris)  # 3

# alternatively the traditional interface:
x <- subset(iris, select = -Species) # 4
y <- Species # 4
model <- svm(x, y) # 4

print(model) #5
summary(model) #6

# test with train data
pred <- predict(model, x) #7
# (same as:)
pred <- fitted(model) #7

# Check accuracy:
table(pred, y) # 7

# compute decision values and probabilities:
pred <- predict(model, x, decision.values = TRUE) # 8
attr(pred, "decision.values")[1:4,] # 8

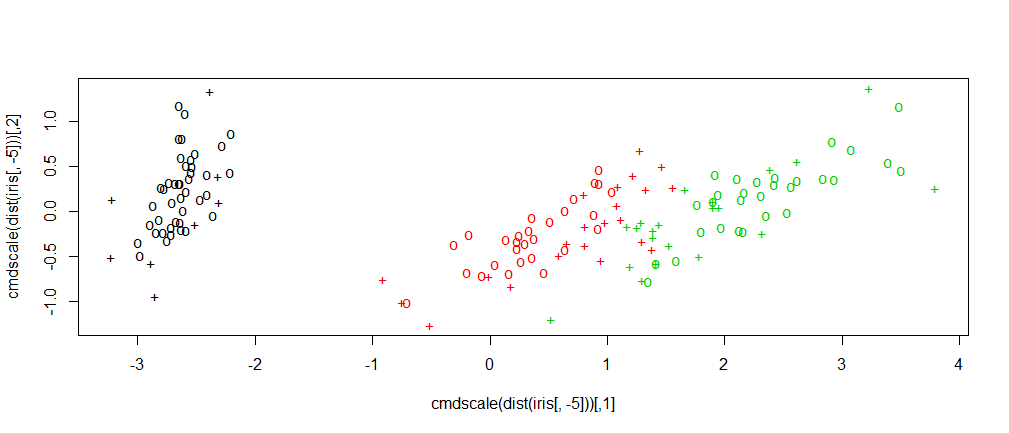
# visualize (classes by color, SV by crosses):
plot(cmdscale(dist(iris[,-5])),
     col = as.integer(iris[,5]),
     pch = c("o","+")[1:150 %in% model$index + 1]) # 9

解释：

• 1.加载数据集iris；
• 2.附加当前数据集，以简化变量名
• 3.使用默认的svm函数，公式：所有的特征影响最后的分类；
• 4.x取前四个特征，y取类别，然后使用svm训练；
• 5.打印模型;

Call:
svm(formula = Species ~ ., data = iris)

Parameters:
   SVM-Type:  C-classification 
 SVM-Kernel:  radial 
       cost:  1 
      gamma:  0.25 

Number of Support Vectors:  51

• 6.描述模型：

Call:
svm(formula = Species ~ ., data = iris)

Parameters:
   SVM-Type:  C-classification 
 SVM-Kernel:  radial 
       cost:  1 
      gamma:  0.25 

Number of Support Vectors:  51

 ( 8 22 21 )

Number of Classes:  3 

Levels: 
 setosa versicolor virginica

• 7.预测

            y
pred         setosa versicolor virginica
  setosa         50          0         0
  versicolor      0         48         2
  virginica       0          2        48

• 8.

  setosa/versicolor setosa/virginica versicolor/virginica
1          1.196152         1.091757            0.6708810
2          1.064621         1.056185            0.8483518
3          1.180842         1.074542            0.6439798
4          1.110699         1.053012            0.6782041

• 9.图形